Question

How much of a 2 gram sample of silver-105 would remain after 86 days? round to three decimal places

Answer 1

We know that the half life of this element is 41.3 days.

We have to find how much will remain of a sample of 2 grams after 86 days.

The half life of 41.3 days means that the mass after 41.3 days will become half of what it was.

We can express this as:

`(M(t+41.3))/(M(t))=(1)/(2)`

As this is represented with an exponential model like this:

`M(t)=M(0)\cdot b^t`

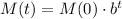
we can use the half-life to find the parameter b:

`\begin{gathered} (M(t+41.3))/(M(t))=(1)/(2) \\ (M(0)\cdot b^(t+41.3))/(M(0)\cdot b^t)=(1)/(2) \\ b^(t+41.3-t)=(1)/(2) \\ b^(41.3)=(1)/(2) \\ b=((1)/(2))^{(1)/(41.3)} \end{gathered}`

Then, knowing that the initial mass M(0) is 2 grams, we can express the final model as:

`M(t)=2\cdot((1)/(2))^{(t)/(41.3)}`

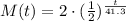
We then can calculate the mass after t = 86 days as:

`\begin{gathered} M(86)=2\cdot((1)/(2))^{(86)/(41.3)} \\ M(86)\approx2\cdot0.236 \\ M(86)\approx0.472 \end{gathered}`

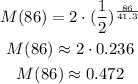
Answer: the mass after 86 days will be 0.472 grams.