ANSWER
Amount = $3102.75
Interest = $1598.75
Step-by-step explanation
The annuity pays 6.6% compounded monthly.
The formula for an Amount compounded at a rate of r after t years is given as:
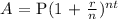
where P = principal (amount deposited) = $1,504
r = rate = 6.6% = 0.066
n = 12 (12 months in a year)
t = number of years = 11 years
Therefore, the amount in the account after 11 years is:
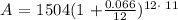
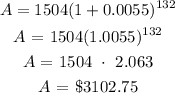
That's the amount in the account after 11 years.
This means that the amount of interest after 11 years is the amount after 11 years minus the amount that was there initially:
Interest = 3102.75 - 1504
Interest = $1598.75