We got to use the Secant-Tangent Theorem, here. It says that AC² is equal to the distance BC times the distance from C to the circumference. Let's denote the point in OC where it intercepts the circumference by D, so:
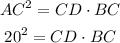
Beucase the radius is equal in all points of the circumference, OA=OB=OD, so BC = OA + OC, and CD = OC - OA. So,
![\begin{gathered} 20^2=CD\cdot BC=(OC-OA)\cdot(OA+OC)=OC^2-OA^2=OC^2-8^2 \\ 20^2=OC^2-8^2 \\ OC^2=20^2+8^2=464 \\ OC=\sqrt[]{464}=21.54\approx22\operatorname{cm} \end{gathered}]()