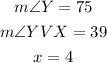Question

Consider parallelogram VWXY below.Use the information given in the figure to find mZY, mZYVX, and x.म7503903xmZY - •mZYVX - _х$12

Answer 1

In a parallelogram, opposite angles are congruent, this means that,

`\begin{gathered} m\angle Y=m\angle W \\ m\angle Y=75 \end{gathered}`

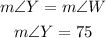
Similarly, in a parallelogram, we have that angles in green are congruent because they are alternate interior angles:

This implies that

`m\angle YVX=39`

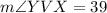
On the other hand, opposite sides are congruent, this implies that

`3x=12`

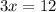
Then, by moving 3 to the right hand side, we get

`\begin{gathered} x=(12)/(3) \\ x=4 \end{gathered}`

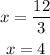
Therefore, the answers are

`\begin{gathered} m\angle Y=75 \\ m\angle YVX=39 \\ x=4 \end{gathered}`