To find the probability that the mean IQ score of people in the sample is less than 98, first we need to convert the value into z-score by using the formula:

Then, when x=98:
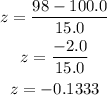
By checking in a standard normal table z=-0.1333 has a p-value=0.4471.
Then the probability is 0.4471 that also can be expressed as 44.71%