Question

Find sinθ, tanθ, and secθ, where θ is the angle shown in the figure. Give exact values, not decimal approximations.sinθ=tanθ=secθ=

Answer 1

1) We have here a right triangle, so we can use the Pythagorean Theorem to find the adjacent leg. Note that the hypotenuse is leg opposite to the right angle. In this case, a=4.

a²=b²+c²

4²=b²+3²

16=b²+9

16-9=b²

b=√7

2) Let's find the trigonometric functions. The first one is the sine (θ), which relates the opposite side and the hypotenuse:

`\sin (\theta)\text{ =}(3)/(4)`

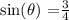
2.2)Moving on, we can deal with the tangent of theta, relating the opposite side over the adjacent, for this one we have to rationalize it:

`\begin{gathered} \tan (\theta)\text{ =}\frac{3}{\sqrt[]{7}} \\ \tan (\theta)=\frac{3\sqrt[]{7}}{7} \end{gathered}`

Finally, let's find the reciprocal function of the cosine function by setting this as the reciprocal of the cosine, and then calculating it:

`\begin{gathered} \sec \text{ (}\theta)=(1)/(\cos(\theta))\Rightarrow\sec (\theta)=\frac{1}{\frac{\sqrt[]{7}}{4}}\Rightarrow\sec (\theta)\text{ =}\frac{4}{\sqrt[]{7}} \\ \sec (\theta)\text{ =}\frac{4\sqrt[]{7}}{7} \end{gathered}`