To determine which option is a representation of the graph we need to make the numer line analysis; to make it we need to notice that the functions has zeros at the points:
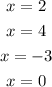
once we know this we divide the number line in the following intervals:
now we need check the sign of the function in each interval, to do this we choose a value in them.
For the first interval let's take x=-4, then we have:
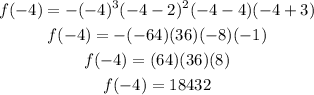
From the last expression we notice that the value of the function is positive at this point. Hence the firts interval have positive values for the function.
For the second interval let's take x=-1, then we have:
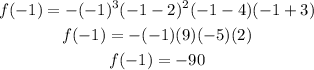
From the result we conclude that the function is negative in this interval.
For the third interval, let's take x=1, we have:
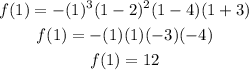
From the result we conclude that the function is positive in this interval.
For the fourth interval, let's take x=3. then we have:
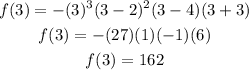
Then the function is positive in this interval.
Finally, for the fifth interval let's take x=5, then we have:
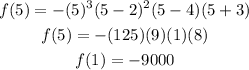
Then the function is negative in the last interval.
Hence the line analysis is:
The y-intercept of the function happens when x=0, then we have that:
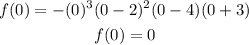
Therefore the y-intercept of the function is 0.
Once we know the information from the line analysis and the y-intercept of the function we conclude that the sketch of the graph is option B.
Two graphs of the function (with different values for the y-axis) are shown below:
This graphs confirm that option B is an approximate sketch of the graph.