To calculate the mass of the product FeCl₃, we will need to do the following steps:
1 - Calculate the molar masses of Cl₂ and FeCl₃.
2 - Calculate the number of moles of Cl₂ in 5g of it.
3 - Calculate the number of moles of FeCl₃ given the stoichiometry of the reaction.
4 - Calculate the mass of FeCl₃ for the calculatd number of moles.
(we will use M for molar mass, m for mass and n for number of moles)
1 - The molar masses can be calculated using the molar masses of the elements in each compound:
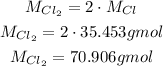
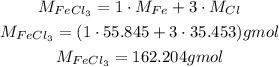
2 - Now, we need to calculate the number of moles of Cl₂, so we will use the molar mass of Cl₂.
So, for the number of moles of Cl₂, we have:
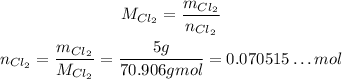
3 - Now, we need to apply the stoichimetry. We can use rule of three for this.
From the balanced equation, we see that for each 3 Cl₂ that react, we will produce 2 FeCl₃.
So, we know that we actually have 0.070515...mol of Cl₂, so we use the rule of three to see how many moles we will produce of FeCl₃:
FeCl₃ --- Cl₂
2 --- 3
n --- 0.070515...mol
So, we have the equation:
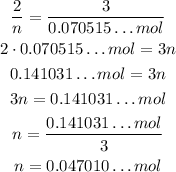
And this is the number of moles of FeCl₃, so we can indicate this with the subscript:
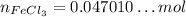
4 - Finally, we will use now the molar mass of FeCl₃ to calculate the mass of 0.047010...mol of FeCl₃. The equation is the same as we used for Cl₂, but we will find the mass instead of the number of moles:
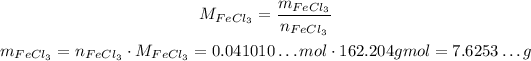
So, the mass is 7.6253...g, but since we started with the mass of 5g, we have only one significant figure, so if we strickly consider the number of significant figures, we need to end up with only one, so:
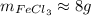
So, the mass that we will produce if all the 5 grams react is 7.6253...g or, approximately 8g.