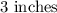Question

A certain television is advertised as a 5-inch TV. If the width of the TV is 4 inches, how many inches tall is the TV

Answer 1

Answer:

The TV is 3 inches tall.

`3\text{ inches}`

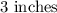
Step-by-step explanation:

Given that the width of the TV is

`4\text{ inches}`

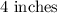
And the TV is 5 inch TV, which means its diagonal is;

`d=5\text{ inches}`

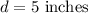
The height of the TV can be calculated using the Pythagoras Theorem;

`\begin{gathered} c^2=a^2+b^2 \\ b=\sqrt[]{c^2-a^2} \end{gathered}`

substituting the diagonal and the width;

`\begin{gathered} b=\sqrt[]{5^2-4^2} \\ b=\sqrt[]{25-16} \\ b=\sqrt[]{9} \\ b=3\text{ inches} \end{gathered}`

Therefore, the TV is 3 inches tall.

`3\text{ inches}`