Question

Write the equation of the perpendicular bisector of XY if endpoint X is at (-9,1) and endpoint Y is at (3,5). A) y = -X B) y = 3x - 6 C) y = -3x - 6 D) y = 3x + 12

Answer 1

A perpendicular bisector is a segment which intersects another segment on its midpoint and with a right angle.

First, we have to find the midpoint between X(-9,1) and Y(3,5), as follows

`\begin{gathered} M=((-9+3)/(2),(1+5)/(2)) \\ M=((-6)/(2),(6)/(2)) \\ M=(-3,3) \end{gathered}`

This means the perpendicular bisector must pass through (-3,3). Now, with the given points we find the slope of XY

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(5-1)/(3-(-9))=(4)/(3+9)=(4)/(12) \\ m=(1)/(3) \end{gathered}`

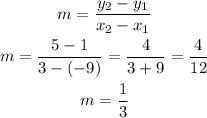
Then, we apply the rule of perpendicularity to find the slope of the perpendicular bisector.

`\begin{gathered} m_1\cdot m=-1 \\ m_1=(-1)/(m) \\ m_1=-(1)/((1)/(3))=-3 \end{gathered}`

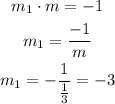
Now, we use the slope-point formula to find the equation for the perpendicular bisector.

`y-y_1=m(x-x_1)`

Where we replace the slope -3 and the point (-3,3).

`\begin{gathered} y-3=-3(x-(-3)) \\ y-3=-3x-9 \\ y=-3x-9+3 \\ y=-3x-6 \end{gathered}`

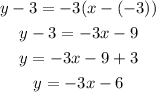
Therefore, the right answer is C.