Answer:
there is no solution (option C)
Step-by-step explanation:
Given:
y > 3/2x - 2
y < 3/2x - 10
To find:
The solution to both graphs
To determine the solution of the graphs, we will consider their slopes
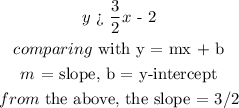
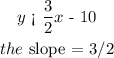
The slope of both inequalities is 3/2. If the slopes of two lines are the same, the lines are said to be parallel. This means both inequalities are parallel lines
For parallel lines, there is no solution because the lines do not intersect (meet).
Since both inequalities give parallel lines, there will be no solution (option C)