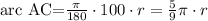Question

Diameters AB and CD of circle K intersect such that mZBKD = 100°.The measure of arc AC isA)80B)260C)100

Answer 1

Let's draw the circle and the lines to see more clear:

The AB and CD are diameters of the circle, so the intersection point K is the center of the circle.

We know the angle BKD=100°, but the angle AKC=BKD because they are opposite angles.

So the measure of arc AC is:

`\begin{gathered} \text{arc AC=}\angle AKC\cdot r \\ \text{where the r is the radius of the circle} \end{gathered}`

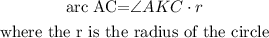
You should note the angle AKC in the above equation must be in radians. To convert degrees to radians use the following equation:

`\angle AKC(radians)=(\pi)/(180)\angle AKC(degrees)`

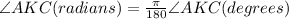
So,

`\text{arc AC=}(\pi)/(180)\cdot100\cdot r=(5)/(9)\pi\cdot r`