Step-by-step explanation
Step 1
set the equations
a)
let x represents the first number
let y represents the second number
so
b) translate:
One number is equal to the square of another, hence
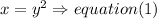
both are positive and their sum is 2450
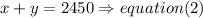
Step 2
solve the equations,
a) replace the x value from equation (1) into equation (2)
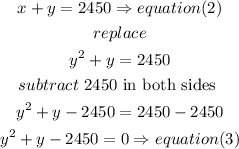
b) now, need to solve the quadratic equation, to do that, we can use the quadratic formula
rememeber:
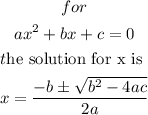
hence