Question

Will bought a new car and financed $14,000 to make the purchase. He financed the car for 72 months with an APR of 6.5%. Assuming he made monthly payments, determine the total interest Will paid over the life of the loan. Round your answer to the nearest cent, if necessary.

Answer 1

The formula for monthly payment is shown below

From the question:

`\begin{gathered} p=\text{ \$14000} \\ r=6.5\text{ \%= 0.065} \\ n=72 \end{gathered}`
`M=(14000((0.065)/(12))(1+(0.065)/(12))^(72))/((1+(0.065)/(12))^(72)-1)`
`\begin{gathered} M=(1400(0.00541667)(1.475427))/(1.475427-1) \\ \\ M=(111.88662)/(0.475427)\text{ = 235.339} \\ M=\text{ \$}235.34 \end{gathered}`

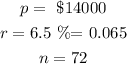
The monthly payment = $235.34

Total amount paid = $235.339 x 72 = $16944.424

Total interest Will paid over the life of the loan = $16944.424 - $14,000 = $2944.424

You are

Thus, Total interest Will paid over the life of the loan = $2944.42 (nearest cent)