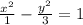SOLUTION
From the question, the center of the hyperbola is
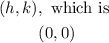
a is the distance between the center to vertex, which is -1 or 1, and
c is the distance between the center to foci, which is -2 or 2.
b is given as
![\begin{gathered} b^2=c^2-a^2 \\ b^2=2^2-1^2 \\ b=\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/96e62v4tbpao228zz6u4hyz9w5uzmayjzc.png)
But equation of a hyperbola is given as
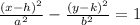
Substituting the values of a, b, h and k, we have
![\begin{gathered} ((x-0)^2)/(1^2)-\frac{(y-0)^2}{\sqrt[]{3}^2}=1 \\ (x^2)/(1)-(y^2)/(3)=1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1cp9d2rvk47w7ff5hgf7e9tnlykkjrwfn8.png)
Hence the answer is