Question

Which of the following is equivalent to sum from n equals 1 to infinity of 10 times quantity negative three eighths end quantity to the power of n?A) 6B)30/11C)- 30/11D)-6

Answer 1

Given: The below

`\sum_{n\mathop{=}1}^(\infty)10(-(3)/(8))^n`

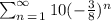
To Determine the sum to infinity of the given

Solution

Letus re-write the give as below

`\sum_{n\mathop{=}1}^(\infty)10(-(3)/(8))^n=10\sum_{n\mathop{=}1}^(\infty)(-(3)/(8))^n`

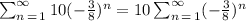
The sum is give by the formula below

`S=(a)/(1-r)`

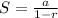
From the given, we can found that a and r is as shown below

`\begin{gathered} a=-(3)/(8) \\ r=-(3)/(8) \end{gathered}`

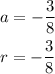
Therefore

`\begin{gathered} S=(a)/(1-r) \\ 1-r=1-(-(3)/(8)) \\ =1+(3)/(8) \\ =(8+3)/(8) \\ =(11)/(8) \\ S=(-(3)/(8))/((11)/(8)) \end{gathered}`
`\begin{gathered} S=-(3)/(8)/(11)/(8) \\ S=-(3)/(8)*(8)/(11) \\ S=-(3)/(11) \end{gathered}`

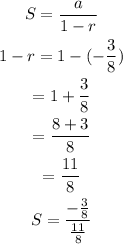
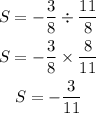
Substituting the sum as shown below

`\begin{gathered} S=\sum_{n\mathop{=}1}^(\infty)(-(3)/(8))^n=-(3)/(11) \\ Therefore \\ 10\sum_{n\mathop{=}1}^(\infty)(-(3)/(8))^n=10*-(3)/(11)=-(30)/(11) \end{gathered}`

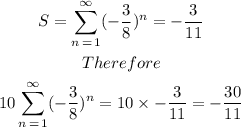
Hence, the equivalent to sum to infinity of the given is -30/11, OPTION C