Question

Find the volume of the sphere . Give the answer in terms of pie and rounded to the nearest cubic foot .The volume in terms of pie is V=_ft3(Simplify your answer . Type an exact answer in terms of pie .)

Answer 1

To answer this question, we need to know the formula for the volume of a sphere. This formula is as follows:

`V_{\text{sphere}}=(4)/(3)\cdot\pi\cdot r^3`

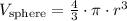
From the figure, we have that the radius, r, is equal to 10 ft. Then, we can, now, calculate the volume of this sphere:

`V_{\text{sphere}}=(4)/(3)\cdot\pi\cdot(10ft)^3=(4)/(3)\cdot\pi\cdot1000ft^3`

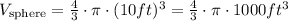
Then, we have:

`V_{\text{sphere}}=(4\cdot1000ft^3)/(3)\cdot\pi=(4000ft^3)/(3)\cdot\pi\Rightarrow V_(sphere)=1333.33333333\pi ft^3`

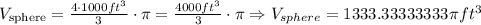
Now, if we rounded this value to the nearest cubic foot, we have that the volume is equal to:

`V_{\text{sphere}}=1333\pi ft^3`

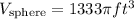
(V = 1333pi ft^3)