The rule of the standard deviation of data is
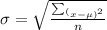
Where n is the number of data
μ is the mean
To find the mean sum of the data given and divide it by n
Since the given data are
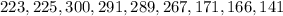
Then n = 9
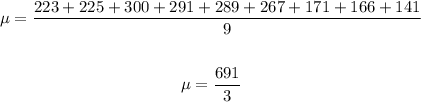
Now, we will subtract the mean from each data, then ann the answers
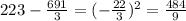
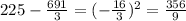
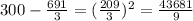
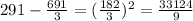
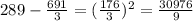
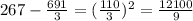
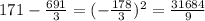
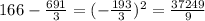
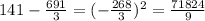
We will add all of these answers and divide them by n
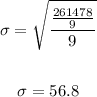
The answer is D