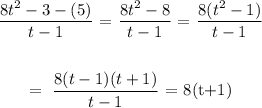ANSWER;
The average rate of change of the function over the given interval is 8(t+1)
EXPLANATION;
The average rate of change of a given function over the interval [a,b] can be represented as;
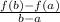
With respect to the question given, a = 1 and b = t

Now, we substitute the expressions in the given rate of change relation above as follows;