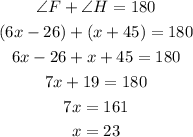Question

Quadrilateral EFGH is inscribed in a circle as shown. m

Answer 1

The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle.

Thus,

• Angle F is ,half, of Arc EHG

,

• Angle H is ,half, of Arc EFG

Together, Arc EHG and Arc EFG makes up a circle. This is equal to 360°.

We can write:

`\begin{gathered} \angle F=(1)/(2)\text{ArcEHG} \\ \angle H=(1)/(2)\text{ArcEFG} \\ \angle F+\angle H=(1)/(2)\text{ArcEHG}+(1)/(2)\text{ArcEFG} \\ \angle F+\angle H=(1)/(2)(ArcEHG+ArcEFG) \\ \angle F+\angle H=(1)/(2)(360) \\ \therefore\angle F+\angle H=180 \end{gathered}`

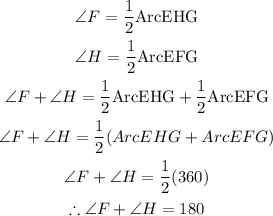
Now, we can substitute the expressions for Angle F and Angle H and solve for x. Shown below:

`\begin{gathered} \angle F+\angle H=180 \\ (6x-26)+(x+45)=180 \\ 6x-26+x+45=180 \\ 7x+19=180 \\ 7x=161 \\ x=23 \end{gathered}`