Question

I will provide another picture, it will be a picture of the questions for this problemPLEASE NOTE THAT THIS IS A LENGTHY PROBLEM (pre calc)

Answer 1

Before we begin, it's important to remember that the formula for the future value in compound interest is:

`A=P(1+(r)/(m))^(mt)`

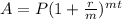
where r = annual rate in decimal form, P = principal, m = number of conversions in a year, and t = time in a year.

Also, the formula for simple interest is:

`Is=\text{Prt}`

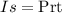
Let's start with Alberto's earnings.

a. $1000 earned 1.2% annual interest compounded monthly.

P = 1,000

r = 0.012

m = 12 (monthly)

t = 10 years

`\begin{gathered} A=1000(1+(0.012)/(12))^(12(10)) \\ A=1000(1.127429249) \\ A=1,127.43 \end{gathered}`

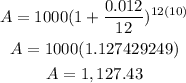
Alberto's $1000 became $1, 127.43 after 10 years.

b. $500 lost 2% over the course of 10 years.

`\begin{gathered} Is=500(0.02)(10) \\ Is=100 \end{gathered}`

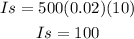
$500 of Alberto lost $100, therefore, it became $400 only.

c. $500 grew compounded continuously at a rate of 0.8% annually.

`\begin{gathered} A=500(1+(0.008)/(1))^(1(10)) \\ A=500(1.082942308) \\ A=541.47 \end{gathered}`

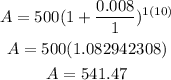
The $500 of Alberto became $541.47.

Therefore, at the end of 10 years, Alberto's money is $1, 127.43 + $400 + $541.47 = $2, 068.90. (Alberto)

Now, let's move to Marie's earnings.

a. $1500 earned 1.4% annual interest compounded quarterly.

P = 1500

r = 1.4% or 0.014

m = 4 (quarterly)

t = 10 years

`\begin{gathered} A=1500(1+(0.014)/(4))^(4(10)) \\ A=1500(1.149992672) \\ A=1,724.99 \end{gathered}`

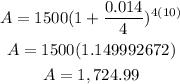
The $1500 of Marie became $1,724.99 after 10 years.

b. $500 gained 4% over the course of 10 years.

`\begin{gathered} Is=\text{Prt} \\ Is=500*0.04*10 \\ Is=200 \end{gathered}`

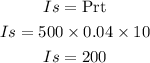
The $500 of Marie gained $200, therefore, it became $700 after 10 years.

To summarize, Marie has $1,724.99 + $700 = $2,424.99 in total after 10 years.

Let's calculate for Hans.

a. $2000 grew compounded continuously at a rate of 0.9% annually.

`\begin{gathered} A=2000(1+(0.009)/(1))^(1(10)) \\ A=2000(1.093733873) \\ A=2,187.47 \end{gathered}`

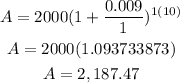
Hans has $2, 187.47 after 10 years.

Lastly, let's see how much Max has.

a. $1000 decrease in value exponentially at a rate of 0.5% annually.

`\begin{gathered} A=1000(1-0.005)^(10)_{}_{} \\ A=1000(0.9511101305) \\ A=951.11 \end{gathered}`

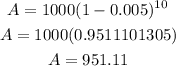
The $1000 of Max became $951.11.

b. $1000 earned 1.8% annual interest compounded biannually (twice a year)

`\begin{gathered} A=1000(1+(0.018)/(2))^(2(10)) \\ A=1000(1.196253785) \\ A=1,196.25 \end{gathered}`

The other $1000 of Max became $1, 196.25.

To summarize, after 10 years, Max has $951.11. + $1, 196.25. = $2,147.36.

To summarize all, the children with their respective balance after 10 years is listed below:

Albert = $2, 068.90

Marie = $2,424.99

Hans = $2, 187.47

Max = $2,147.36

Marie has the most money and will be awarded $10,000.