SOLUTION
Given the question in the question tab, the following are the solution steps to answer the question.
STEP 1: Write the given quadratic equation.
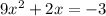
STEP 2: Express the equation in the standard quadratic form
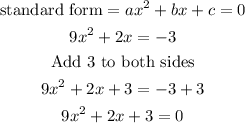
STEP 3: Write the quadratic formula
![x_1,x_2=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/xjo82o7e0ug0fgwgd2uqnuhekhnu5pfftu.png)
STEP 4: Write the needed parameters to substitute into the formula
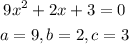
STEP 5: Substitute the values into the formula and solve for x
![\begin{gathered} x_(1,2)=(-2\pm√(2^2-4\cdot\:9\cdot\:3))/(2\cdot\:9) \\ \text{simplify }\sqrt[]{2^2-4\cdot\: 9\cdot\: 3} \\ \sqrt[]{2^2-4\cdot\: 9\cdot\: 3}=\sqrt[]{4-108}=\sqrt[]{-104}=2√(26)i \\ x_(1,\: 2)=\frac{-2\pm\sqrt[]{2^2-4\cdot9\cdot3}}{2\cdot\: 9}=(-2\pm\:2√(26)i)/(2\cdot\:9) \\ \mathrm{Separate\: the\: solutions} \\ x_1=(-2+2√(26)i)/(2\cdot\:9),\: x_2=(-2-2√(26)i)/(2\cdot\:9) \\ \frac{-2+2\sqrt[]{26}i}{2\cdot\: 9}=-(1)/(9)+\frac{\sqrt[]{26}}{9}i_{} \\ \frac{-2-2\sqrt[]{26}i}{2\cdot\: 9}=-(1)/(9)-\frac{\sqrt[]{26}}{9}i \\ x=-(1)/(9)+\frac{\sqrt[]{26}}{9}i\text{ or }-(1)/(9)-\frac{\sqrt[]{26}}{9}i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/s2e5ajaikw7yozdexwmo7yoasl772lmtn8.png)
Hence, the roots of the equations are:
![\begin{gathered} x_1=-(1)/(9)+\frac{\sqrt[]{26}}{9}i \\ x_2=-(1)/(9)-\frac{\sqrt[]{26}}{9}i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/xsee0pz7mrs8yg4ziezv96phianwiow3cy.png)