1 Answer

ManoDestra · Answer 1 · 2023-11-25T19:32:59+0000

Assuming a linear relationship between X and Y, find the slope of the line to write down an equation of the form:

where m is the slope of the line and b is the y-intercept.

Take two pairs of values to calculate the slope. Use the pairs (2,8) and (4,14):

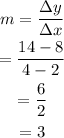
$\begin{gathered} m=(\Delta y)/(\Delta x) \\ =(14-8)/(4-2) \\ =(6)/(2) \\ =3 \end{gathered}$

Substitute m=3 into the equation, as well as the values of one of the pairs. Take x=2 and y=8. You can then find the value of b:

$\begin{gathered} 8=3(2)+b \\ =6+b \\ \Rightarrow b=2 \end{gathered}$

Substitute b=2 and m=3 to find the equation of that linear relation:

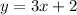
Substitute x=7 to find the missing value of y:

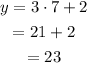
$\begin{gathered} y=3\cdot7+2 \\ =21+2 \\ =23 \end{gathered}$

Therefore, the equation of the table is y=3x+2 and the missing value of y when x=7 is 23.

Please log in or register to add a comment.