Question

A. This is an exponential situation because the population is increasing each year by a percentage of the previous year. Complete the table below based on the growth rate of 1.1%. Some of the entries are done for you. Round projected populations to 2 decimal places. (there is a graph i am going to send)B. Write an exponential equation for the world population growth after 2010. Let P = the projected population in billions and t = the number of years after 2010. Hint: Think about how you calculated the entries in the table. If you started with 6.9 billion each time, how could you calculate each population? Think back to your work in the lesson.__________C .Use your model to predict the population in 2020.______ billion

Answer 1

Given: The population growth rate in 2010 and the population of people in 2010

`\begin{gathered} rate=1.1\% \\ Population=6.9billion \end{gathered}`

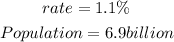
To Determine: The value of the space shown in the table

Solution

The modelled growth rate formula is

`\begin{gathered} P=P_0(1+r)^t \\ P_0=Initial-population \\ r=growth-rate \\ t=time \\ P=Present-population \end{gathered}`
`\begin{gathered} P=6.9billion*1.1 \\ P=7.59billion \end{gathered}`

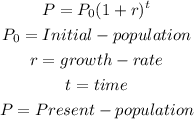
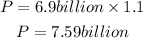
The projected population is 2011 is 7.59 billion

In 2012, the number of year after 2010 would be

`t=2012-2010=2`

The projected population in 2012 would be

`\begin{gathered} P=1.1*7.59billion \\ P=8.349billion \\ P\approx8.35billion \end{gathered}`

In 2013, the number of year after 2010 would be

`\begin{gathered} t=2013-2010 \\ t=3years \end{gathered}`

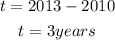
The projected population in 2013 would be

`\begin{gathered} P=1.1*8.349billion \\ P=9.1839billion \\ P\approx9.18billion \end{gathered}`

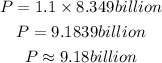
The table is filled as shown below