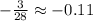To answer the item (a), we should first define what is a fair game. By definition, a fair game is a game in which there is an equal chance of winning or losing. We can say that if a game is fair then the probability of winning is equal to the probability of losing.
For this game, we have a chance of winning of 1/28, and since we have only the options of winning and losing, losing represents a chance of 27/28.
Since
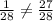
This is not a fair game.
Now, for item (b), if we play several times, the most probable distribution for every 28 times you play is 1 win and 27 losses, which will result in 25 dollars for the win and minus 27 dollars for the losses, then the total would be minus 3 dollars for every 28 games. If you play several times you're going to lose some money!
As I stated in the last paragraph, in a total of 28 games you're going to get - 3 dollars, so to get the net winning for each round you just divide the value by the total of games.