Question

You buy a new computer for $2100. The computer decreases by 50% annually. When will the computer have a value of $600?(Please show your work as I take notes for future problems)

Answer 1

1 year and 10 months or 1.8 years

Step-by-step explanation

We have that the price of the new computer is $2100 and it decreases by 50% annually.

This means it is a compound decrement.

So, we can apply the formula:

`A=P(1-R)^t`

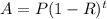
where A = price after t years

P = initial price

R = rate of decrease

t = amount of years

Therefore, we have that:

A = $600

P = $2100

R = 50%

Therefore, we need to find t:

`\begin{gathered} 600\text{ = 2100(1 - }(50)/(100))^t \\ (600)/(2100)=(1-0.5)^t \\ 0.2857=0.5^t \\ \text{ Find the logarithm of both sides:} \\ \log (0.2857)=log(0.5)^t\text{ = t }\cdot\text{log0.5} \\ -0.5441=\text{ t }\cdot\text{ (-0.301)} \\ t\text{ = }(-0.5441)/(-0.301) \\ t\text{ = 1.8 years or 1 year and 10 months} \end{gathered}`

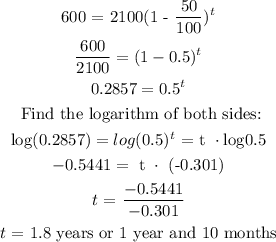
The computer will have a value of $600 after 1 year and 10 months.