Question

According to a recent report, the average American consumes 22.7 teaspoons of sugar each day (Cohen, August 2013). Assuming that the distribution is approximately normal with a standard deviation of = 4.5, find each of the following values.What percent of people consume more than 32 teaspoons of sugar a day?P(X > 32)= %

Answer 1

1.94%

Explanation:

From the given information:

• The average number of teaspoons of sugar consumed each day = 22.7

,

• Standard deviation = 4.5

We want to find the percentage of people who consume more than 32 teaspoons of sugar a day.

In order to do this, first, we find the z-value at X=32 using the z-score formula.

`\begin{gathered} z-\text{score}=(X-\mu)/(\sigma) \\ At\text{ X=32, }z-\text{score}=(32-22.7)/(4.5)=(9.3)/(4.5)=2.0667 \end{gathered}`

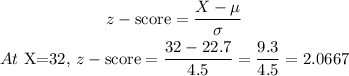
Next, from the z-score table:

`P\mleft(x>2.0667\mright)=0.019381=1.9381\%`

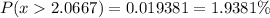
Approximately 1.94% of people consume more than 32 teaspoons of sugar a day.