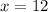Question

I want to know what the value of x is and how do i get the value of x

Answer 1

We need to find the value of x.

We know that the polygons are similar.

Also, similar polygons have proportional sides. Thus, the ratio between two sides of the polygon on the left equals the ratio between the equivalent sides of the polygon on the right.

Then, we can write:

`\begin{gathered} (PN)/(LM)=(KJ)/(GH) \\ \\ (x)/(6)=(8)/(4) \\ \\ (x)/(6)=2 \\ \\ 6\cdot(x)/(6)=6\cdot2 \\ \\ x=12 \end{gathered}`

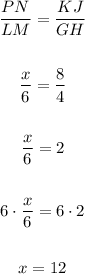
Therefore:

`x=12`