To find the perimeter of a quadrilateral, we need to add the lengths of the sides. For this, we use the distance formula:

Let's solve for each of the sides.
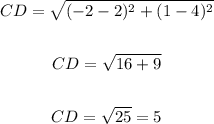

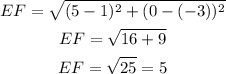

So each of the sides of the quadrilateral measures 5 units.
The perimiter is the sum of all the sides. P =5 + 5 + 5 + 5 = 4 x 5 = 20 units.