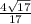Question

Is anyone available to help with a challenging trig/pre-calc problem?

Answer 1

To solve the present question, we will use the following definition:

`cos(a+b)=cos(a)\cdot cos(b)-sin(a)\cdot sin(b)`

To do so, we will use the following values:

`a=b=(\theta)/(2)`

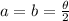
which will lead us to the following:

`\begin{gathered} cos((\theta)/(2)+(\theta)/(2))=cos((\theta)/(2))\cdot cos((\theta)/(2))-sin((\theta)/(2))\cdot sin((\theta)/(2)) \\ \\ cos(\theta)=cos²((\theta)/(2))-sin²((\theta)/(2)) \end{gathered}`

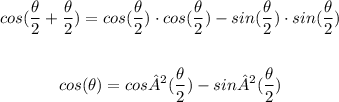
but, from any value of angle, we have the following relation:

`sin²(\omega)+cos²(\omega)=1`

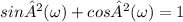
and this allow us to write:

`cos²((\theta)/(2))=1-sin²((\theta)/(2))`

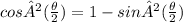
and substituting it in the equation we found, we have the following:

`\begin{gathered} cos(\theta)=1-sin²((\theta)/(2))-sin²((\theta)/(2)) \\ \\ cos(\theta)=1-2sin²((\theta)/(2)) \\ \\ sin((\theta)/(2))=\pm\sqrt{(1-cos(\theta))/(2)} \end{gathered}`

Because the angle lies from π/2 and π, half of it will lie from π/4 and π/2, which means that the sine of this angle can only be positive. From this fact and by substituting the value of cosine we have in the equation we developed, we have the following solution:

`\begin{gathered} sin((\theta)/(2))=\sqrt{(1-(-(15)/(17)))/(2)} \\ \\ sin((\theta)/(2))=\sqrt{(1+(15)/(17))/(2)} \\ \\ sin((\theta)/(2))=\sqrt{((17)/(17)+(15)/(17))/(2)}=\sqrt{(32)/(2\cdot17)}=\sqrt{(16)/(17)}=\sqrt{(17\cdot16)/(17²)}=(4√(17))/(17) \\ \\ sin((\theta)/(2))=(4√(17))/(17) \end{gathered}`

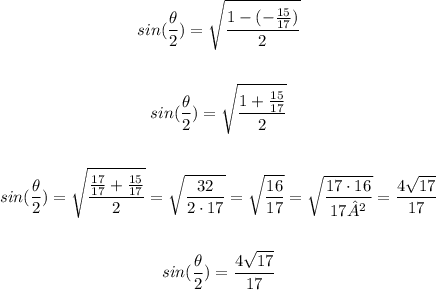
From the solution developed above, we are able to conclude that the answer to the present problem is the first one:

`(4√(17))/(17)`