We are given the following three functions
Linear function:
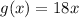
Quadratic function:
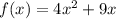
Exponential function:
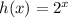
We are asked that which function grows at the fastest rate for increasing values of x?
The function g(x) is a linear function, it will grow at the slowest rate for increasing values of x.
The function f(x) is a quadratic function, it will grow faster than the linear function but slower than the exponential function.
The function h(x) is an exponential function, it will grow exponentially meaning that it will grow faster than the linear and the quadratic function.
Let us have a look at the graph of these functions for a better understanding.
Therefore, the function h(x) grows at the fastest rate for increasing values of x.
The correct answer is option C.