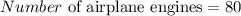Question

O POLYNOMIAL AND RATIONAL FUNCTIONSWord problem involving the maximum or minimum of a quadrati...

Answer 1

Given that the unit cost of manufacturing airplane engines in an aircraft factory is expressed by the function:

`\begin{gathered} C(x)=1.2x^2-192x+20026 \\ where \\ C\Rightarrow cost\text{ in dollars} \\ x\Rightarrow number\text{ of engines made} \end{gathered}`

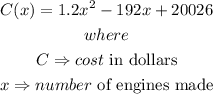
To evaluate the number of engines to be made so as to minimize the unit cost,

step 1: Take the derivative of C(x) with respect to x.

`C^(\prime)(x)=(dC(x))/(dx)=2.4x-192`

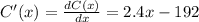
step 2: Evaluate the critical or stationary point of the C(x) function.

At, the stationary point, the derivative of C(x) equals zero.

Thus, at the critical point,

`\begin{gathered} C^(\prime)(x)=0 \\ where \\ C^(\prime)(x)=2.4x-192 \\ \Rightarrow2.4x-192=0 \\ add\text{ 192 to both sides of the equation} \\ 2.4x-192+192=0+192 \\ \Rightarrow2.4x=192 \\ divide\text{ both sides by the coefficient of x, which is 2.4} \\ (2.4x)/(2.4)=(192)/(2.4) \\ \Rightarrow x=80 \end{gathered}`

step 3: Take the second derivative of the C(x) function to determine the extreme points of the C(x) function.

`C^(\prime)^(\prime)(x)=(d^2C(x))/(dx)=2.4`
`\begin{gathered} when\text{ C''\lparen x\rparen<0, we have a maximum point} \\ when\text{ C''\lparen x\rparen>0, we have a minimum point} \end{gathered}`

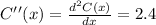
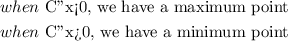
Since the second derivative of C(x) is evaluated to be greater than zero, this implies that we have a minimum point or value of C(x).

Thus, for C(x) to be a minimum, we have the value of x to be 80.

Hence, number of engines to be made so as to minimize the unit cost is

`Number\text{ of airplane engines}=80`