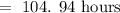SOLUTION:
Step 1:
In this question, we are given the following:
Fluorescent light bulbs have lifetimes that follow a normal distribution, with an average life of 1,276 days and a standard deviation of 1,595 hours. In the production process, the manufacturer draws random samples of 231 lightbulbs and determines a sample's mean lifetime. What is the standard deviation, in hours, of this sample mean?
Step 2:
The details of the solution are as follows:
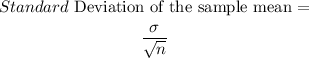
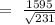
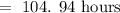
CONCLUSION:
The standard deviation, in hours, of the sample mean =