Question

a coffee distributor needs to mix an organic free-trade coffee blend that normally sells for $9.80 per pound with an Arabian mocha coffee blend that normally sells for $13.70 per pound to create 40 lb of a coffee can sell for $12.63 per pound how many pounds of each kind of coffee should they mix?

Answer 1

We can create the following system of equations with the information given:

Let x be the number of pounds of Organic free-trade coffee

Let y be the number of pounds of Arabian mocha coffee

`\begin{gathered} 9.8x+13.7y=12.63\cdot40\text{ (1)} \\ x+y=40\text{ (2)} \end{gathered}`

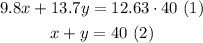
Now, we can use the substitution method to isolate y in (2) and substituting into (1):

`y=40-x\text{ (2)}`
`\begin{gathered} 9.8x+13.7(40-x)=505.2 \\ 9.8x+548-13.7x=505.2 \\ -3.9x=505.2-548 \\ -3.9x=-42.8 \\ x=(42.8)/(3.9) \\ x=10.97 \\ x\approx11 \end{gathered}`

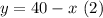
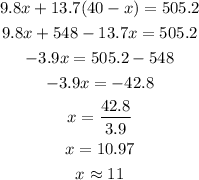
Then, since we have the x-value (number of pounds for Organic free-trade), we can substitute into (2):

`\begin{gathered} y=40-11 \\ y=29 \end{gathered}`

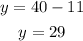
Therefore, the coffee distributor would need 11 pounds of Organic free-trade and 29 pounds of Arabian mocha coffee.