Question

A bag contains four red marbles and sixblue marbles. You randomly pick amarble and then pick a second marblewithout returning the marbles to the bag.Both marbles are red.

Answer 1

Given:

The number of red marbles in the bag = 4 marbels.

The number of blur marbles in the bag = 6 marbles.

We pick a marble and then pick a second marble without returning the marble to the bag.

Aim:

We need to find the probability of getting both marbles are red.

Step-by-step explanation:

The number of marble in the bag = the number of red marble + the number of blue marbles.

The number of marble in the bag = 4+6 =10 marbles.

`n(S)=10`

The number of red marbles in the bag =4.

`n(R)=4`

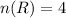
The probability of getting red marbles is P(R).

`P(R)=(n(R))/(n(S))=(6)/(10)=(3)/(5)`

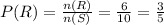
After picking one marble from the bag, Now the number of marble in the bag = 10-1 =9 marbles.

`n(S_1)=9_{}`

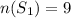
The picked marble is red.

The number of red marbles in the bag =3.

`n(R_1)=3`

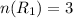
The probability of getting red marble a second time

`P(R_1)=(3)/(9)=(1)/(3)`

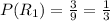
The probability of getting both marbles are red is

`P(R\text{ and R)=P(R)}* P(R_1)`

`P(R\text{ and R)=}(3)/(5)*(1)/(3)`

`P(R\text{ and R)=}(1)/(5)`

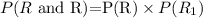
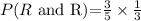
Final answer:

Probability = 1/5.