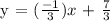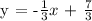Let's make an equation that represents the linear function passing through points (1,2) and (4,1) by Slope-Intercept Form.

In making an equation in this form, we must first determine the value of the slope (m) and the y-intercept (b) of the line.
For determining the value of the slope, we use this formula,
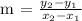
Let's substitute (x1,y1) = (1,2) and (x2,y2) = (4,1), we get,
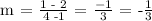
Let's now compute for the value of the y-intercept (b),
m = -1/3 and (x1,y1) = (1,2)
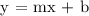
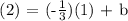
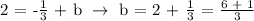
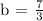
Let's now make the equation substituting the value of m and b.
m = -1/3 and b = 7/3