The formula for the perimeter of the base (square) is ,
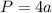
where,
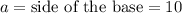
Therefore,
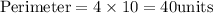
Let us now solve for the slant height(l),
To solve for l, we will make use of Pythagoras theorem
![\begin{gathered} 13^2=l^2+5^2 \\ 169=l^2+25 \\ 169-25=l^2 \\ 144=l^2 \\ \Rightarrow l^2=144 \\ l=\sqrt[]{144}=12\text{units} \\ l=12\text{units} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1dx0nll5a37ycshnh1p4o2xm8yccho94xe.png)
Hence, the slant height is 12units.
The formula for the Lateral Area(LA) is given as,
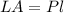
Therefore,
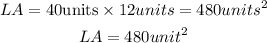
Hence, the Lateral area is 480unit².
The formula for the Surface area(SA) is,
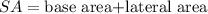
where the base area(B) is,
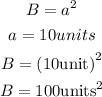
Hence, the Surface area is,
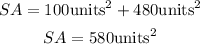
Hence, the Surface area is 580unit².