Question

Find the area of an equilateral triangle with a height that measures 9 feet

Answer 1

Given

The height of an equilateral triangle is, 9 feet.

To find the area of an equilateral triangle

The area of an equilateral triangle is,

`A=(1)/(2)\cdot b\cdot h`

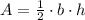
Since h=9 feet.

Then the value of b is measured using pythagoras theorem.

`\begin{gathered} a^2=h^2+((a)/(2))^2 \\ a^2=h^2+(a^2)/(4) \\ a^2-(a^2)/(4)=h^2 \\ (3)/(4)a^2=h^2 \end{gathered}`

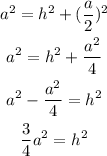
Then for h=9,

`\begin{gathered} 9^2=(3)/(4)a^2 \\ 81\cdot(4)/(3)=a^2 \\ a^2=27\cdot4 \\ a=\sqrt[]{9\cdot3\cdot4} \\ a=6\sqrt[]{3} \end{gathered}`

Then the area will be,

`\begin{gathered} A=(1)/(2)\cdot b\cdot h \\ A=(1)/(2)\cdot a\cdot h \\ A=(1)/(2)\cdot6\sqrt[]{3}\cdot9 \\ A=27\sqrt[]{3}=46.77sq.feet \end{gathered}`