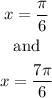We need to isolate x, then, by moving 15 to the right hand side, we get
![\tan x=\frac{5\sqrt[]{3}}{15}](https://img.qammunity.org/2023/formulas/mathematics/college/cpw8m7pv07y2gbn6frbvy3x9l0jfpvpy66.png)
which gives
![\tan x=\frac{\sqrt[]{3}}{3}=\frac{1}{\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/m05ixis6avb4hmz9mqve6tqvnzwmw99m46.png)
By applying the inverse of the tangent function, we have
![x=\tan ^(-1)(\frac{1}{\sqrt[]{3}})](https://img.qammunity.org/2023/formulas/mathematics/college/vbxjn1zixq1a1tiapdtj2fwor1cs6wasqt.png)
Now, we need to find which angle corresponds to the inverse tangent of 1 over square root of 3. From the unit circle:
we can see that
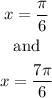
are equivalent to
![\tan ^(-1)(\frac{1}{\sqrt[]{3}})](https://img.qammunity.org/2023/formulas/mathematics/college/1ujzifo2ewvk97c2qup0c6mrdkb3jcnqu6.png)
Therefore, the answers are