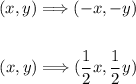From the figure, we have the coordinates of the vertices:
• ABC ==> A(0, 4), B(2, 0), C(0, 0)
• A'B'C' ==> A'(0, -2), B'(-1, 0), C'(0, 0)
Let's determine the sequence of transformations which shows that ABC is similar to A'B'C'.
The sequence of transformation which occured here is a rotation followed by a dilation.
For the rotation, apply the rules of rotation:
180 degrees rotation: (x, y) ==> (-x, -y)
We now have the coordinates:
(0, -4), (-2, 0), (0, 0)
Then for the dilation, let's find the scale factor.
To find the scale factor, divide the corresponding coordinates of A'B'C' by that of ABC:
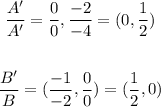
Therefore, the scale factor of the dilation is (1/2, 0)
Therefore, the sequence of transformations which shows that ABC is similar to A'B'C' are: