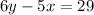Answer
The equation of the line is:
SOLUTION
Problem Statement
The question gives us a point on a line (-1, 4) and a slope of 5/6 and we are required to find the equation of the line.
Method
To find the equation of a line, we use the point-slope equation formula given below:
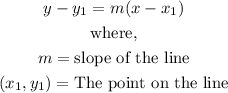
Implementation

Final Answer
The equation of the line is: