Answer:
decay factor = 0.82
percent change = 18%
Function: h(m) = 15400(0.82)^m
Value after 8 years = $3147.97
Step-by-step explanation:
If the copier depreciates by 18% each year, the decay factor will be:
d = 1 - r = 1 - 0.18 = 0.82
Because r is the rate of depreciation.
On the other hand, the percent change will be the rate of depreciation, so it is equal to 18%.
Finally, the function has the following form:
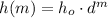
Where h0 is the initial value of the copier and d is the decay factor. So, the function for the value of the copier is:
h(m) = 15400(0.82)^m
Finally, the value of the copier 8 years after can be calculated replacing m by 8, so:
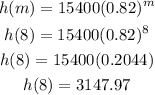
So, the value after 8 years will be $3147.97
Therefore, the answers are:
decay factor = 0.82
percent change = 18%
Function: h(m) = 15400(0.82)^m
Value after 8 years = $3147.97