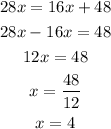1) If l and m are parallel, the correspondent interior angles have to be the same.
In this case, we have 65 degrees for l.
The correspondent angle for m is the complement of 115 degrees.
To calculate the value of this angle we have to do:
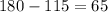
As both correspondent angles are equal in value, the lines are parallel.
2) In this case, we do not know if they are parallel, as we don't know at which angles the line l intersect the other.
We know only the angles for m.
3) As both correspondent angles are equal (in this case, both are rectangular), we can conclude that they are parallel.
4) We have to compare correspondent angles.
The opposite angles by the vertex have the same value.
In that case, we start by opposing the angle for l, and we discover then that it is the same angle that its correspondent in m.
7) In this case, the correspondent angles need to satisfy:
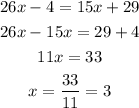
9) In this case:
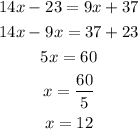
11) In this case, the angles are complementary: the sum of both angles has to be 180 degrees. So we can write:
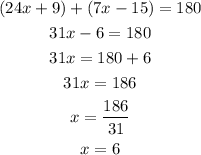
13) We can look at it graphically:
By this graph we can see that the angle 28x has to be equal to the sum of the angle 48 and the angle 16x in order for l and m to be parallel.
Then, we write the equation: