Given:
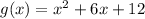
And given interval is
![[a,b]=[-3,5]](https://img.qammunity.org/2023/formulas/mathematics/college/65b68nixjixttnvce4btilpw2u4j2g2fqm.png)
Required:
To find the average rate of change of the given function over the interval −3≤x≤5.
Step-by-step explanation:
To calculate the average rate of change between the 2 points use.
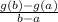
Here,
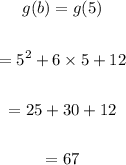
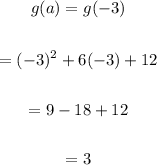
Therefore,
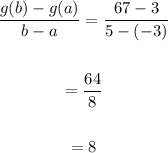
Final Answer:
The average rate of change of the function over the interval −3≤x≤5 is 8.