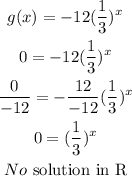Question

Select all the correct answers, Exponential function fis represented by the table. 0 1 D B 4 -4 10 22 Function gis represented by the equation. gir) Which statements are true about the two functions? The functions have the same y-intercept. Both functions are increasing on all intervals of x. Both functions approach - as approaches - Both functions approach the same value as x approaches The functions have the same x-intercept.

Answer 1

1) True

2) False

3) True

4) False

5) False

Analyzing the table and the function g(x)= -12(1/3)^x

We can see that:

The y-intercept is given when x=0

So, (0, -12) and :

`\begin{gathered} g(x)=-12((1)/(3))^x \\ g(0)=-12((1)/(3))^0 \\ g(0)=-12(1) \\ g(0)\text{ =-12} \end{gathered}`

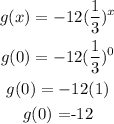
1) So both functions have the same y-intercept (y= -12).

Checking the second option:

`\begin{gathered} g(0)\text{ =-12} \\ g(1)=-12((1)/(3))^1,\text{ g(1)=-4} \\ g(2)=-12((1)/(3))^2=-(12)/(9)=-(4)/(3) \\ g(3)\text{ =-0.44} \\ g(4)=-0.142 \\ g(-1)\text{ =-}36 \end{gathered}`

2)So, as we can see both functions are increasing on this interval ([0,4], but not in every interval of x. False, since g(x) is a decreasing function.

3) For f(x) and g(x) this is true. since according to this graph we can see that the end behavior

Notice that as x approaches -∞, f(x) approaches -∞ as well as g(x). True

4) That's false too since both functions approach different values as x approaches infinity.

5) No, they do not have the same x-intercept. f(x), has x=2, and g(x) no.

`\begin{gathered} g(x)=-12((1)/(3))^x^{}_{} \\ 0=-12((1)/(3))^x \\ (0)/(-12)=-(12)/(-12)((1)/(3))^x \\ 0=((1)/(3))^x \\ No\text{ solution in R} \end{gathered}`