In standard form, the equation of a parabola is:
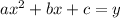
We have three points, and we evaluate this equation for these three points. For the point (1, -3):

For (3, 9):
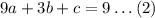
For (4, 18):
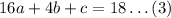
Now, subtracting (1) from (2) and (3):

Solving this system of equations leads to ((5) - (4)):
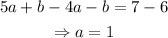
Now, using this result in (4):
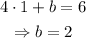
Finally, using a and b in (1):
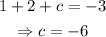
The standard form of the parabola passing through the three points (1,-3), (3,9), and (4,18) is:
