Question

A bullet of mass 19.6 grams is fired with a speed of 318 meters per second toward a wood block of mass 269 grams initially at rest on a very smooth surface. What is the change in momentum of the bullet if it becomes embedded in the block? Answer must be in 3 significant digits.

Answer 1

We are given that a bullet travels at a speed of 318 m/s and hits a wooden block and starts to move embedded in the block (smooth surface). To determine the change in momentum we need first to determine the final velocity of the bullet. To do that we will use the fact that the kinetic energy of the system is preserved, therefore:

`(1)/(2)m_bv^2_(0b)+(1)/(2)m_Bv^2_(0B)=(1)/(2)m_bv^2_(fb)+(1)/(2)m_Bv^2_(fB)`

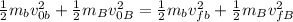
Where:

`\begin{gathered} m_b=\text{ mass of the bullet} \\ m_B=\text{ mass of the block} \\ v_(0b)=\text{ initital velocity of the bullet} \\ v_(0B)=\text{ initial velocity of the Block} \\ v_(fb)=\text{ final velocity of the bullet} \\ v_(fB)=\text{ final velocity of the block} \end{gathered}`

Now, since the block is initially at rest this means that its initial velocity is zero, therefore:

`(1)/(2)m_bv^2_(0b)=(1)/(2)m_bv^2_(fb)+(1)/(2)m_Bv^2_(fB)`

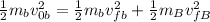
We can also cancel out the 1/2:

`m_bv^2_(0b)=m_bv^2_(fb)+m_Bv^2_(fB)`

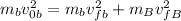
Now, since the bullet is embedded in the block this means that their final velocities are equal, therefore, we can rewrite the equation as:

`m_bv^2_(0b)=m_bv^2_f+m_Bv^2_f`

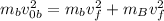
Taking the final velocity as a common factor we get:

`m_bv^2_(0b)=(m_b+m_B)v^2_f`

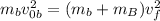
Now we solve for the final velocity by dividing both sides by the masses:

`(m_bv^2_(0b))/(\mleft(m_b+m_B\mright))=v^2_f`

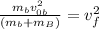
Now we take square root to both sides:

`\sqrt{(m_bv^2_(0b))/((m_b+m_B))}=v^{}_f`

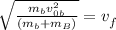
Now we simplify:

`v_{0b\text{ }}\sqrt[]{(m_b)/((m_b+m_B))}=v^{}_f`

Now we plug in the given values:

`(318(m)/(s))_{}\sqrt[]{((19.6g))/(((19.6g)+(269g)))}=v^{}_f`

Solving the operations we get:

`82.87(m)/(s)=v_f`

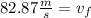
Now that we have the final velocity we can use the following formula for the change in momentum of an object:

`\Delta P=m(v_f-v_0)`

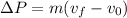
Where:

`\begin{gathered} \Delta P=\text{ change in momentum} \\ m=\text{ mass} \\ v_0=\text{ initial velocity} \\ v_f=\text{ final velocity} \end{gathered}`

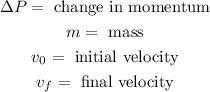
Replacing the values we get:

`\Delta P=(19.6g)(82.87(m)/(s)-318(m)/(s))`

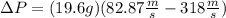
Now we solve the operations:

`\Delta P=-4608.548g(m)/(s)`

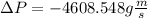
Therefore, the change in momentum is -4608.548 g*m/s.