Question

Complete the function table.
y = -3x + 5
х у
-4||
-2
10
2
4

Answer 1

The graph of the original function is:

The question asks us to find the value of the new graph.

In the orignal graph, when x = 0, y = 1 i.e:

`\begin{gathered} y=2^x \\ \text{when,} \\ x=0 \\ y=2^0=1 \end{gathered}`

This is the value for the original graph.

In the question we are asked, the value of y when x = 0 is not 1. This means that the graph has been shifted to the right.

Whenever a graph has been shifted to the right by n units, you must subtract n from the x-term of the function.

Let us put this into mathematics:

`\begin{gathered} y=2^(x-n) \\ \text{where n is the number of units the graph was shifted to the right} \\ \\ \end{gathered}`

In order to find the value of n, we need to study the new graph and substitute a coordinate point from it into the new equation above.

From studying the new graph, when x = 1, y = 1 as well. Hence, we can find n using this coordinate

`\begin{gathered} y=2^(x-n) \\ \text{when,} \\ x=1,y=1 \\ 1=2^(1-n) \\ 1=2*2^(-n) \\ \text{divide both sides by 2} \\ (1)/(2)=2^(-n) \\ 2^(-1)=2^(-n) \\ \\ \therefore-1=-n\text{ (Divide both sides by -1)} \\ n=1 \end{gathered}`

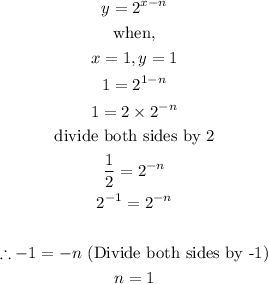
Therefore, the new graph is:

`\begin{gathered} y=2^(x-1) \\ y=2^x*2^(-1) \\ y=0.5(2^x)\text{ (Option A)} \end{gathered}`