Question

For the functions ƒ(x) = log8(x) and g(x) = log5(x), for what values of x is ƒ(x) > g(x)?A. 0 < x < 1B. 1 < x < ∞C. 0 < x < 5D. 0 < x < 8

Answer 1

Given

`f(x)=\log_8(x)\text{ and }g(x)=\log_5(x)`

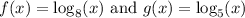
To have a better understanding of how the function behaves, let graph the function.

f(x) = g(x) when x = 1

So we consider the interval (0, 1) and (1, ∞)

From the graph, f(x) > g(x) in the interval (0, 1) while f(x) < g(x) in the interval (1, ∞)

Therefore, the values of x for which f(x) > g(x) is 0 < x < 1

The correct option is A.