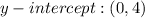Question

Graph f(x) = 4 (0.5). Then determine which answer choice matches the graph you drew. Find the y-intercept of the function.Identify the solution that has the correct graph and the correct y-intercept.

Answer 1

GIVEN:

We are given the following function;

`f(x)=4(0.5)`

Required;

To graph the function and then find the y-intercept.

Step-by-step solution;

The function given is in the form;

`f(x)=ab^x`

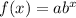
This is an exponential function and x can take any value, which will determine the value of y. From the function we can determine that the initial value a is the point where x = 0 and at that point we have the y intercept, that is, when x = 0, then y = a.

`\begin{gathered} y=ab^x \\ \\ When\text{ }x=0. \\ \\ y=ab^0 \\ \\ y=a(1) \\ \\ y=a \end{gathered}`

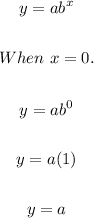
Therefore, for the function given;

`\begin{gathered} f(x)=4(0.5)^x \\ \\ When\text{ }x=0, \\ \\ f(x)=4(0.5)^0 \\ \\ f(x)=4(1) \\ \\ f(x)=4 \end{gathered}`

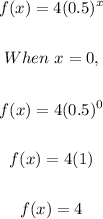
Therefore, the y-intercept here is 4. Note also that the value of b is 0.5, which is less than 1. This indicates that its an exponential decrease (exponential decay). Therefore, its downward sloping from left to right

The graph is shown below;

Therefore,

ANSWER:

Option C is the correct answer.

`y-intercept:(0,4)`